Бинарные деревья
Определение
Бинарное (двоичное) дерево (binary tree) - это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла.
Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева.
Узел дерева, не имеющий потомков, называется листом.
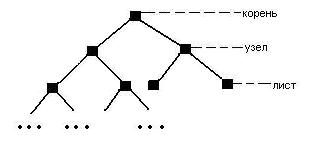
Схематичное изображение бинарного дерева
Бинарное дерево может представлять собой пустое множество.
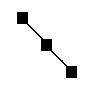
Бинарное дерево может выродиться в список
Построение бинарного дерева
Сначала мы должны определить структуру для создания корня и узлов дерева:
template<class T>
struct TNode {
T value;
TNode *pleft, *pright;
//constructor
TNode() {
pleft = pright = 0;
}};
Здесь поля pleft и pright - это указатели на потомков данного узла, а поле value предназначено для хранения информации.
Теперь мы можем написать рекурсивную функцию, которая будет вызываться при создании дерева:
template<class T>
void makeTree(TNode<T>** pp, T x) {
if(!(*pp)) {
TNode<T>* p = new TNode<T>();
p->value = x;
*pp = p;
}
else {
if((*pp)->value > x)
makeTree(&((*pp)->pleft), x);
else
makeTree(&((*pp)->pright), x);
}}
Эта функция добавляет элемент x к дереву, учитывая величину x. При этом создается новый узел дерева.
Обход дерева
Функция, выполняющая обход дерева, позволяет перебрать все элементы, содержащиеся в дереве.
В приведенной ниже реализации функция обхода дерева будет просто выводить на экран значение поля value каждого узла дерева (включая его корень):
template<class T>
void walkTree(TNode<T>* p) {
if(p) {
walkTree(p->pleft);
cout << p->value << ' ';
walkTree(p->pright);
}}
При работе с деревьями обычно используются рекурсивные алгоритмы. Использование рекурсивных функций менее эффективно, поскольку многократный вызов функции расходует системные ресурсы. Тем не менее, в данном случае использование рекурсивных функций является оправданным, поскольку нерекурсивные функции для работы с деревьями гораздо сложнее и для написания, и для восприятия кода программы.
Например, нерекурсивная функция для обхода дерева может выглядеть так:
template<class T>
void walkNotRec(TNode<T>* tree) {
if (tree) {
TNode<T> temp;
TNode<T>* ptemp = &temp;
TNode<T>* p = ptemp, *c = tree, *w;
while (c != ptemp) {
cout << c->value;
w = c->pleft;
c->pleft = c->pright;
if(c == p)
c->pright = 0;
else
c->pright = p;
p = c;
if (w) c = w;
}
}}
Применение
Организация данных с помощью бинарных деревьев часто позволяет значительно сократить время поиска нужного элемента. Поиск элемента в линейных структурах данных обычно осуществляется путем последовательного перебора всех элементов, присутствующих в данной структуре. Поиск по дереву не требует перебора всех элементов, поэтому занимает значительно меньше времени. Максимальное число шагов при поиске по дереву равно высоте данного дерева, т.е. количеству уровней в иерархической структуре дерева.
Оставить комментарий
Комментарии


деревья, сохранять их и работать с ними. Писал программу для
старшеклассников, т.к. они работали вслепую с деревьями.
Скачать можно тут:
https://soft.softodrom.ru/ap/Trees-Portable-p19987 или
http://fish1821.narod.ru/Programs.html


