Красно-черные деревья

Двоичные деревья работают лучше всего, когда они сбалансированы, когда длина пути от корня до любого из листьев находится в определенных пределах, связанных с числом узлов. Красно-черные деревья - один из способов балансировки деревьев. Название происходит от стандартной раскраски узлов таких деревьев в красный и черный цвета. Цвета узлов используются при балансировке дерева. Во время операций вставки и удаления поддеревья может понадобиться повернуть, чтобы достигнуть сбалансированности дерева. Оценкой как среднего время, так и наихудшего является O(lg n).

Этот раздел - один из наиболее трудных в данной книжке. Если вы ошалеете от вращений деревьев, попробуйте перейти к следующему разделу о слоёных списках. Прекрасно написанные разделы о красно-черных деревьях вы найдете у Кормена[1990].

Теория

Красно-черное дерево - это бинарное дерево с следующими свойствами:

• Каждый узел покрашен либо в черный, либо в красный цвет.
• Листьями объявляются NIL-узлы (т.е. "виртуальные" узлы, наследники узлов, которые обычно называют листьями; на них "указывают" NULL указатели). Листья покрашены в черный цвет.
• Если узел красный, то оба его потомка черны.
• На всех ветвях дерева, ведущих от его корня к листьям, число черных узлов одинаково.

Количество черных узлов на ветви от корня до листа называется черной высотой дерева. Перечисленные свойства гарантируют, что самая длинная ветвь от корня к листу не более чем вдвое длиннее любой другой ветви от корня к листу. Чтобы понять, почему это так, рассмотрим дерево с черной высотой 2. Кратчайшее возможное расстояние от корня до листа равно двум - когда оба узла черные. Длиннейшее расстояние от корня до листа равно четырем - узлы при этом покрашены (от корня к листу) так: красный, черный, красный, черный. Сюда нельзя добавить черные узлы, поскольку при этом нарушится свойство 4, из которого вытекает корректность понятия черной высоты. Поскольку согласно свойству 3 у красных узлов непременно черные наследники, в подобной последовательности недопустимы и два красных узла подряд. Таким образом, длиннейший путь, который мы можем сконструировать, состоит из чередования красных и черных узлов, что и приводит нас к удвоенной длине пути, проходящего только через черные узлы. Все операции над деревом должны уметь работать с перечисленными свойствами. В частности, при вставке и удалении эти свойства должны сохраниться.

Вставка

Чтобы вставить узел, мы сначала ищем в дереве место, куда его следует добавить. Новый узел всегда добавляется как лист, поэтому оба его потомка являются NIL-узлами и предполагаются черными. После вставки красим узел в красный цвет. После этого смотрим на предка и проверяем, не нарушается ли красно-черное свойство. Если необходимо, мы перекрашиваем узел и производим поворот, чтобы сбалансировать дерево.

Вставив красный узел с двумя NIL-потомками, мы сохраняем свойство черной высоты (свойство 4). Однако, при этом может оказаться нарушенным свойство 3, согласно которому оба потомка красного узла обязательно черны. В нашем случае оба потомка нового узла черны по определению (поскольку они являются NIL-узлами), так что рассмотрим ситуацию, когда предок нового узла красный: при этом будет нарушено свойство 3. Достаточно рассмотреть следующие два случая:

• Красный предок, красный "дядя": Ситуацию красный-красный иллюстрирует рис. 3.6. У нового узла X предок и "дядя" оказались красными. Простое перекрашивание избавляет нас от красно-красного нарушения. После перекраски нужно проверить "дедушку" нового узла (узел B), поскольку он может оказаться красным. Обратите внимание на распространение влияния красного узла на верхние узлы дерева. В самом конце корень мы красим в черный цвет корень дерева. Если он был красным, то при этом увеличивается черная высота дерева.

 
• Красный предок, черный "дядя": На рис. 3.7 представлен другой вариант красно-красного нарушения - "дядя" нового узла оказался черным. Здесь узлы может понадобиться вращать, чтобы скорректировать поддеревья. В этом месте алгоритм может остановиться из-за отсутствия красно-красных конфликтов и вершина дерева (узел A) окрашивается в черный цвет. Обратите внимание, что если узел X был в начале правым потомком, то первым применяется левое вращение, которое делает этот узел левым потомком.

Каждая корректировка, производимая при вставке узла, заставляет нас подняться в дереве на один шаг. В этом случае до остановки алгоритма будет сделано 1 вращение (2, если узел был правым потомком). Метод удаления аналогичен.
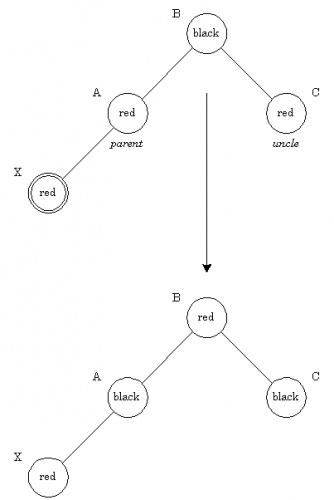
Рис. 3.6: Вставка - Красный предок, красный "дядя"


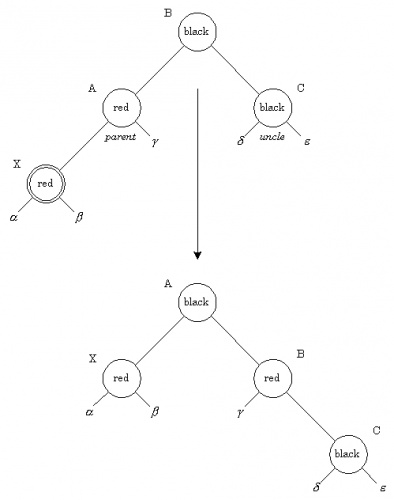
Рис. 3.7: Вставка - красный предок, черный "дядя"

Реализация

Коды, реализующие работу с красно-черными деревьями на Си находится в разделе 4.7. Операторы typedef T, а также сравнивающие compLT и compEQ следует изменить так, чтобы они соответствовали данным, хранимым в узлах дерева. В каждом узле типа Node хранятся указатели left, right на двух потомков и parent на предка. Цвет узла хранится в поле color и может быть либо RED, либо BLACK. Собственно данные хранятся в поле data. Все листья дерева являются "сторожевыми" (sentinel), что сильно упрощает коды. Узел root является корнем дерева и в самом начале является сторожевым.

Функция insertNode запрашивает память под новый узел, устанавливает нужные значения его полей и вставляет в дерево. Соответственно, она вызывает insertFixup, которая следит за сохранением красно-черных свойств. Функция deleteNode удаляет узел из дерева. Она вызывает deleteFixup, которая восстанавливает красно-черные свойства. Функция findNode ищет в дереве нужный узел.

---

Оглавление

Оставить комментарий

Комментарий: можно использовать BB-коды Максимальная длина комментария - 4000 символов.	CodeNet ВКонтакте Facebook Twitter Google Яндекс Чтобы оставить комментарий, необходимо авторизоваться. Можно ввести логин и пароль, или авторизоваться через социальные сети.