CodeNet / Приложения / Алгоритмы / Сортировка / Сортировка и поиск: Рецептурный справочник
Сортировка Шелла
Метод, предложенный Дональдом Л. Шеллом, является неустойчивой сортировкой по месту. Эффективность метода Шелла объясняется тем, что сдвигаемые элементы быстро попадают на нужные места. Среднее время для сортировки Шелла равняется O(n1.25), для худшего случая оценкой является O(n1.5). Дальнейшие свойства см. в книжке Кнута [1998].
Теория
На рис. 2.2(a) был приведен пример сортировки вставками. Мы сначала вынимали 1, затем сдвигали 3 и 5 на одну позицию вниз, после чего вставляли 1. Таким образом, нам требовались два сдвига. В следующий раз нам требовалось еще два сдвига, чтобы вставить на нужное место 2. На весь процесс нам требовалось 2 + 2 + 1 = 5 сдвигов.
На рис. 2.2(b) иллюстрируется сортировка Шелла. Мы начинаем, производя сортировку вставками с шагом 2. Сначала мы рассматриваем числа 3 и 1: извлекаем 2, сдвигаем 3 на 1 позицию с шагом 2, вставляем 2. Затем повторяем то же для чисел 5 и 2: извлекаем 2, сдвигаем вниз 5, вставляем 2. И т.д. Закончив сортировку с шагом 2, производим ее с шагом 1, т.е. выполняем обычную сортировку вставками. Всего при этом нам понадобится 1 + 1 + 1 = 3 сдвига. Таким образом, использовав вначале шаг, больший 1, мы добились меньшего числа сдвигов.
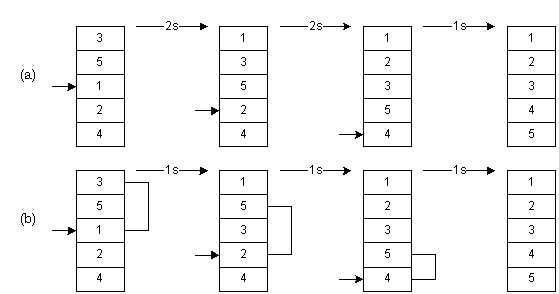
Рис. 2-2: Сортировка Шелла
Можно использовать самые разные схемы выбора шагов. Как правило, сначала мы сортируем массив с большим шагом, затем уменьшаем шаг и повторяем сортировку. В самом конце сортируем с шагом 1. Хотя этот метод легко объяснить, его формальный анализ довольно труден. В частности, теоретикам не удалось найти оптимальную схему выбора шагов. Кнут[1] провел множество экспериментов и нашел следующую формулу выбора шагов h для массива длины N:
Вот несколько первых значений h:
h1 = 1
h2 = (3 x 1) + 1 = 4
h3 = (3 x 4) + 1 = 13
h4 = (3 x 13) + 1 = 40
h5 = (3 x 40) + 1 = 121
Чтобы отсортировать массив длиной 100, прежде всего найдем номер s, для которого hs >= 100. Согласно приведенным цифрам, s = 5. Нужное нам значение находится двумя строчками выше. Таким образом, последовательность шагов при сортировке будет такой: 13-4-1. Ну, конечно, нам не нужно хранить эту последовательность: очередное значение h находится из предыдущего по формуле
Реализация
В реализации сортировки Шелла на Си следует изменить операторы typedef T и сравнения compGT так, чтобы они соответствовали данным, хранимым в массиве. Основная часть алгоритма - сортировка вставками с шагом h.
