CodeNet / Приложения / Графика / Учебник по компьютерной графике
Компьютерная Графика
- Алгоритм Кируса-Бека.
- Формализованный алгоритм Кируса-Бека.
- Разбиение невыпуклых многоугольников.
- Последовательное отсечение многоугольников.Алгоритм Сазермана - Ходтмена.
- Невыпуклые отсекающие области. Алгоритм Вейлера - Айдертона.
Алгоритм Кируса-Бека.
Есть область ( видимая или невидимая ) и через неё проходит отрезок.
Исходные данные : выпуклая область отсечения.
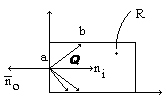( рис. 1 )Алгоритм Кируса - Бека работает только с выпуклыми областями.
Используем понятие - внутренняя нормаль, т.е. если любая (o) принадлежит ребру, (o) b в другой границе окна, то произведение м.б. любым внутренним вектором на внутренней нормали, проведенной из этой же (o), будет положительно т.к. любой угол < 90 градусов.
Если применить к внешней нормали, то
Произведение вектора на внешнюю нормаль будет всегда отрицательным.
Пусть есть отрезок ( P1, P2) ( рис.2 ) , представим его в параметрическом виде.
P(t) = P1 + ( P2 - P1 ) t , где t - параметр ( расстояние от начальной (o) до конечной (o))
Пусть какая-то точка F будет являться граничной точкой окна, тогда из вышесказанного мы можем сказать, что для любого отрезка ( P1, P2 ) справедливо следующие :
Выводы:
1. Бесконечная прямая пересекает замкнутую выпуклую область ровно в двух точках и это справедливо для n - мерного пространства.
2. Пусть эти 2 точки не принадлежит одному ребру или граничной плоскости, тогда выражение n[ P(t) - F ] = 0 будет иметь только одно решение.
3. Если точка F принадлежит ребру для которого вектор n внутренняя нормаль, то точка P(t) будет являться точкой пересечения данного отрезка с указанной граничной плоскостью.
Пример 1. Частично видимый отрезок.
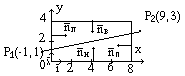(рис.2)Уравнение прямой P1P2 = 0,2( X - 6 ).
Запишем этот отрезок в параметрическом виде т.е.:
i, j - нормальные единичные вектора.
Зададим в окне нормали
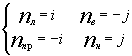
а) Для удобства вычисления допустим, что (o) F = (0,0), тогда [ P(t) - F ] = (10t - 1 )i + (2t + 1)j.
Рассмотрим произведение nл[ P(t) - F] = 10t - 1 = 0 t = 0,1.
Подставляем t в наше параметрическое уравнение, т.е. P(0,1) = [-1,1] + [10,2] 0,1 = [0,1 , 2].
б) Берем точку F = (8,4).
Опять находим вектор.
Для nн, nв параметр t не лежит в заданной области. Эти точки t нам не нужны.
Подставляем t = 0,9 в параметрическое уравнение P(0,9) = [ 8, 2,8]
Отсюда следует, что видимый участок лежит в пределах 0,1<t<0,9 или [0;1,2] -:- [8;2,8].
Пример 2. Нетривиальный невидимый отрезок.
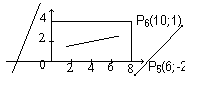(рис. 3)
P5P6 не является тривиально невидимым.
л -3/2 = t; п 1/2 = t; н 2/3 = t; в 2 = t; - не верно => важна ориентация отрезка.
Если взять ориентацию отрезка P5 => P6, то получается что отрезок пересекает сначала правое, а затем нижнее ребро, но такого быть не может => такие параметры не подходят.
Из приведенного выше примера следует, что для правильного подбора параметров, нужно учитывать ориентацию отрезка.
Предыдущий раздел | Предыдущая тема | Следующая тема | Следующий раздел |