Фракталы вокруг нас
Математика,
если на нее правильно посмотреть,
отражает не только истину,
но и несравненную красоту.
Бертранд Рассел.
Вы, конечно же, слышали о фракталах. Вы, конечно же, видели эти захватывающие картинки из Bryce3d более реальные, чем сама реальность. Горы, облака, кора дерева - все это выходит за рамки привычной евклидовой геометрии. Мы не можем описать камень или границы острова с помощью прямых, кружков и треугольников. И здесь нам приходят на помощь фракталы. Что же это за знакомые незнакомцы? Когда они появились?
История появления.
Первые идеи фрактальной геометрии возникли в 19 веке. Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Пеано нарисовал особый вид линии (рисунок №1). Для ее рисования Пеано использовал следующий алгоритм.

На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длинна исходной линии (Часть 1 и 2 рисунка 1). Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано. Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек (размерность 0). А кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость. Во многих других областях науки появлялись задачи, решение которых приводило к странным результатам, на подобие описанных выше (Броуновское движение, цены на акции).
Отец фракталов
Вплоть до 20 века шло накопление данных о таких странных объектах, без какой либо попытки их систематизировать. Так было, пока за них не взялся Бенуа Мандельброт - отец современной фрактальной геометрии и слова фрактал. Работая в IBM математическим аналитиком, он изучал шумы в электронных схемах, которые невозможно было описать с помощью статистики. Постепенно сопоставив факты, он пришел к открытию нового направления в математике - фрактальной геометрии.
Что же такое фрактал. Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). И одно из определений фрактала - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого (по крайней мере, приблизительно).
Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б.Мандельброта "The Fractal Geometry of Nature" ("Фрактальная геометрия природы") ставший классическим - "Какова длина берега Британии?". Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Померив берег с помощью километровой линейки мы получим какую-то длину. Однако мы пропустим много небольших заливчиков и полуостровков, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до, скажем, 1 метра - мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и измерим длину берега с помощью миллиметровой линейки, мы тут учтем детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно - длина берега Британии бесконечна.
Немного о размерностях.
В своей повседневной жизни мы постоянно встречаемся с размерностями. Мы прикидываем длину дороги (250 м), узнаем площадь квартиры (78 м2) и ищем на наклейке объем бутылки пива (0.33 дм3). Это понятие вполне интуитивно ясно и, казалось бы, не требует разъяснения. Линия имеет размерность 1. Это означает, что, выбрав точку отсчета, мы можем любую точку на этой линии определить с помощью 1 числа - положительного или отрицательного. Причем это касается всех линий - окружность, квадрат, парабола и т.д.
Размерность 2 означает, что любую точку мы можем однозначно определить двумя числами. Не надо думать, что двумерный - значит плоский. Поверхность сферы тоже двумерна (ее можно определить с помощью двух значений - углов наподобие ширины и долготы).
Если смотреть с математической точки зрения, то размерность определяется следующим образом: для одномерных объектов - увеличение в два раза их линейного размера приводит к увеличению размеров (в данном случае длинны) в два раза (2^1).
Для двумерных объектов увеличение в два раза линейных размеров приводит к увеличению размера (например, площадь прямоугольника) в четыре раза (2^2).
Для 3-х мерных объектов увеличение линейных размеров в два раза приводи к увеличению объема в восемь раз (2^3) и так далее.
Таким образом, размерность D можно рассчитать исходя из зависимости увеличения "размера" объекта S от увеличения линейных размеров L. D=log(S)/log(L). Для линии D=log(2)/log(2)=1. Для плоскости D=log(4)/log(2)=2. Для объема D=log(8)/log(2)=3. Может быть немного запутано, но в общем-то несложно и понятно.
Зачем я это все рассказываю? А для того чтобы понять, как отделять фракталы от, скажем, колбасы. Попробуем посчитать размерность для кривой Пеано. Итак, у нас исходная линия, состоящая из трех отрезков длинны Х, заменяется на 9 отрезков втрое меньшей длинны. Таким образом, при увеличении минимального отрезка в 3 раза длина всей линии увеличивается в 9 раз и D=log(9)/log(3)=2 - двумерный объект!!!
Так вот, когда размерность фигуры получаемой из каких-то простейших объектов (отрезков) больше размерности этих объектов - мы имеем дело с фракталом.
Фракталы делятся на группы. Самые большие группы это:
- геометрические фракталы
- алгебраические фракталы
- системы итерируемых функций
- стохастические фракталы.
Геометрические фракталы.
Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется "затравка" - аксиома - набор отрезков, на основании которых будет строиться фрактал. Далее к этой "затравке" применяют набор правил, который преобразует ее в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем (по крайней мере, в уме) бесконечное количество преобразований - получим геометрический фрактал.
Рассмотренная выше кривая Пеано является геометрическим фракталом. На рисунке ниже приведены другие примеры геометрических фракталов (слева направо Снежинка Коха, Лист, Треугольник Серпинского).

Снежинка Коха

Лист

Треугольник Серпинского
Из этих геометрических фракталов очень интересным и довольно знаменитым является первый - снежинка Коха. Строится она на основе равностороннего треугольника. Каждая линия которого ___ заменяется на 4 линии каждая длинной в 1/3 исходной _/\_. Таким образом, с каждой итерацией длинна кривой увеличивается на треть. И если мы сделаем бесконечное число итераций - получим фрактал - снежинку Коха бесконечной длинны. Получается, что наша бесконечная кривая покрывает ограниченную площадь. Попробуйте сделать то же самое методами и фигурами из евклидовой геометрии.
Размерность снежинки Коха (при увеличении снежинки в 3 раза ее длина возрастает в 4 раза) D=log(4)/log(3)=1.2619...
Для построения геометрических фракталов хорошо приспособлены так называемые L-Systems. Суть этих систем состоит в том, что имеется определенных набор символов системы, каждый из которых обозначает определенное действие и набор правил преобразования символов. Например, описание снежинки Коха с помощью L-Systems в программе Fractint
; Adrian Mariano from The Fractal Geometry of Nature by Mandelbrot
Koch1 {
;устанавливаем угол поворота 360/6=60 градусов
Angle 6
; Начальный рисунок для построения
Axiom F--F--F
; Правило преобразования символов
F=F+F--F+F
}
В данном описании геометрические значения символов следующие:
F обозначает прочертить отрезок + поворот по часовой стрелке - поворот против часовой стрелки
Второе свойство фракталов - самоподобие. Возьмем, например, треугольник Серпинского. Для его построения из центра равностороннего треугольника "вырежем" треугольник. Повторим эту же процедуру для трех образовавшихся треугольников (за исключением центрального) и так до бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и увеличим его - получим точную копию целого. В данном случае мы имеем дело с полным самоподобием.
Сразу оговорюсь, что большинство рисунков фракталов в данной статье получены с помощью программы Fractint. Если Вас заинтересовали фракталы, то это программа must have для Вас. С ее помощью можно строить сотни различных фракталов, получить исчерпывающую информацию по ним, и даже послушать как фракталы звучат ;).
Сказать, что программа хороша - значит ничего не сказать. Она великолепна, за исключением одного но - последняя версия 20.0 доступна только в варианте для DOS :(. Вы сможете найти эту программу (последняя версия 20.0) на
http://spanky.fractint.org/www/fractint/fractint.html.
Алгебраические фракталы.
Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:
- С течением времени стремится к бесконечности.
- Стремится к 0
- Принимает несколько фиксированных значений и не выходит за их пределы.
- Поведение хаотично, без каких либо тенденций.
Чтобы проиллюстрировать алгебраические фракталы обратимся к классике - множеству Мандельброта.
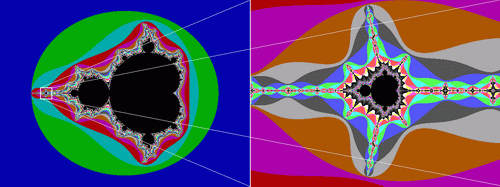
Для его построения нам необходимы комплексные числа. Любой уважающий себя язык программирования включает в себя инструментарий для работы с комплексными числами, а даже если и нет, то их несложно запрограммировать и самим, и на крайний случай (а таких, я думаю, будет большинство :)) у нас есть Fractint которая все посчитает и нарисует за нас.
На всякий случай напомню, что такое комплексные числа. Комплексное число - это число, состоящее из двух частей - действительной и мнимой, и обозначается оно a+bi. Действительная часть a это обычное число в нашем представлении, а вот мнимая часть bi интересней. i - называют мнимой единицей. Почему мнимой? А потому, что если мы возведем i в квадрат, то получим -1.
Комплексные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень, нельзя только их сравнивать. Комплексное число можно изобразить как точку на плоскости, у которой координата Х это действительная часть a, а Y это коэффициент при мнимой части b.
Функционально множество Мандельброта определяется как Zn+1=Zn*Zn+C. Для построения множества Мандельброта воспользуемся алгоритмом на псевдо Бейсике (легко для понимания и перевода на любимые языки).
For a=-2 to 2 ' для всех действительных а от -2 до 2 For b=-2 to 2 ' для всех мнимых b от -2 до 2 С=a+bi Z0=0+0i 'Принадлежит множеству Мандельброта Lake=True 'Повторяем 255 раз (для режима 256 цветов) For iteration=1 to 255 Zn=Z0*Z0+C 'Проверили - не принадлежит If abs(Zn)>2 then Lake=False: Exit For Z0=Zn Next 'Нарисовали черную точку,принадлежащую "озеру" Мандельброта. If Lake=True Then PutPixel(a,b,BLACK) ' Нарисовали точку не принадлежащую множеству или лежащую на границе. Else PutPixel(a, b, iteration) Next Next
А теперь опишу программку словами. Для всех точек на комплексной плоскости в интервале от -2+2i до 2+2i выполняем некоторое достаточно большое количество раз Zn=Z0*Z0+C, каждый раз проверяя абсолютное значение Zn. Если это значение больше 2, что рисуем точку с цветом равным номеру итерации на котором абсолютное значение превысило 2, иначе рисуем точку черного цвета. Все множество Мандельброта в полной красе у нас перед глазами.
Черный цвет в середине показывает, что в этих точках функция стремится к нулю - это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. А самое интересное это границы множества. Они то и являются фрактальными. На границах этого множества функция ведет себя непредсказуемо - хаотично.
Меняя функцию, условия выхода из цикла можно получать другие фракталы. Например, взяв вместо выражения С=a+bi выражение Z0=a+bi, а С присваивать произвольные значения мы получим множество Жюлиа, тоже красивый фрактал.
На рисунке, изображающем множество Мандельброта я взял небольшой участок и увеличил его до размеров всего экрана (как в микроскоп). Что же мы видим? Проявление самоподобности. Не точной самоподобности, но близкой и с ней мы будем сталкиваться постоянно, увеличивая части нашего фрактала больше и больше. До каких же пор мы можем увеличивать наше множество? Так вот если мы увеличим его до предела вычислительной мощности компьютеров, то покроем площадь равную площади солнечной системы вплоть до Сатурна.
Стохастические фракталы.
Типичный представитель данного класса фракталов "Плазма".

Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далеенаходим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок. Если мы теперь скажем, что цвет точки это высота над уровнем моря - получим вместо плазмы - горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму строится карта высот, к ней применяются различные фильтры, накладываем текстуру и пожалуйста фотореалистичные горы готовы.

Системы итерируемых функций (IFS - Iterated Function Systems)
Эта группа фракталов получила широкое распространение благодаря работам Майкла Барнсли из технологического института штата Джорджия. Он пытался кодировать изображения с помощью фракталов. Запатентовав несколько идей по кодированию изображений с помощью фракталов, он основал фирму "Iterated Systems", которая через некоторое время выпустила первый продукт "Images Incorporated", в котором можно было изображения переводить из растровой формы во фрактальную FIF. Это позволяло добиться высоких степеней сжатия. При низких степенях сжатия качество рисунков уступало качеству формата JPEG, но при высоких картинки получались более качественными. В любом случае этот формат не прижился, но работы по его усовершенствованию ведутся до сих пор. Ведь этот формат не зависит от разрешения изображения. Так как изображение закодировано с помощью формул, то его можно увеличить до любых размеров и при этом будут появляться новые детали, а не просто увеличится размер пикселей. Хуже это или лучше - решать надо в каждом отдельном случае.

Если в L-systems (алгебраических фракталах) речь шла о замене прямой линии неким полигоном, то в IFS мы в ходе каждой итерации заменяем некий полигон (квадрат, треугольник, круг) на набор полигонов, каждый их которых подвергнут аффинным преобразованиям. При аффинных преобразованиях исходное изображение меняет масштаб, параллельно переносится вдоль каждой из осей и вращается на некоторый угол.
В результате можно получить потрясающие коэффициенты сжатия. Например рисунок папоротника кодируется с помощью 28!!! цифр и один и тот же рисунок получается в не зависимости от того что взяли за основу - прямоугольник, круг, треугольник или что-либо еще. Но к сожалению процесс создания набора коэффициентов для произвольного изображения очень трудоемок и занимает очень много времени.

Фракталы и хаос.
Понятие фрактал неразрывно связано с понятием хаос. Хаос - это отсутствие предсказуемости. Хаос возникает в динамических системах, когда для двух очень близких начальных значений система ведет себя совершенно по-разному. Пример хаотичной динамической системы - погода. Метеорологи шутят: "Взмах крыла бабочки в Техасе приводит к урагану во Флориде". Поэтому, когда будете слушать следующий прогноз погоды перед полетом на самолете вспомните эту статью :)
Хорошо проиллюстрировать хаотичное поведение можно с помощью так называемого logistic equation x=c*x(1-x). Пришло это выражение из биологии, т.к. это грубая модель популяции животных. Так вот при исследовании поведения этой функции выяснилась интересная ее особенность. Если с - фактор роста популяции находится в пределах от 1 до 3, то через некоторое количество итераций популяция стабилизируется.

При с=3 наша функция раздваивается - через определенное число итераций приходим к ситуации, когда высокая популяция в один год сменяется низкой в следующий и значение выражения как бы скачет между двумя значениями.
При с=3.45 она раздваивается снова и у нас уже имеется четырехлетний цикл.
Далее при росте с функция раздваивается все быстрее и быстрее: при с=3.54, с=3.564, с=3.569 ...
И в точке 3.57 начинается хаос. Значения выражения не имеют какой либо периодичности или структуры. На рисунке изображена зависимость поведения функции от величины с.
Ну и на закуску интересный пример. Вы ведь доверяете своему компьютеру? Я имею в виду вы считаете, что он очень точная и быстрая машина. Тогда запустите Microsoft Excel. Введите в ячейки А1 и B1 значение 4. В ячейки A2 и B2 одинаковые значения между 0 и 1. В ячейку A3 введите формулу "=$A$1*A2*(1-A2)", а в ячейку B3 введем ту же формулу, только раскроем скобки "=$B$1*(B2-B2*B2)", а в ячейку С3 поместим формулу разности "=A3-B3". Как и следовало ожидать результаты в ячейках A3 и B3, а разница равна 0. Теперь выделяем диапазон A3:C3 и копируем его в нижние 100 строк и смотрим что у нас происходит. Начиная с 5-7 строки мы видим, что появилась небольшая разница в результате 2 формул. Эта разница довольно быстро возрастает и на 50 шагу эта разница уже по величине равна нашим числам. Более того разные процессоры будут давать разные результаты. Возникает закономерный вопрос: какое же значение верно? Правильный ответ: "Никакое!". Начиная с определенного места ВСЕ современные компьютеры дают неверный результат. Вот такой простой задачкой мы поставили нашего "мистера-точность" в тупик :(.
Еще раз вспомните про прогноз погоды и самолеты. А ведь это только цветочки...
Вот и подошла к концу наша экскурсия в мир фракталов. Надеюсь она Вам понравилась. Я только немного приоткрыл Вам завесу в мир фракталов.
Если хотите изучить фракталы поподробнее зайдите на страничку http://www.eclectasy.com/fractovia/. Вы найдете там десятки программ рисования фракталов, некоторые с хорошими объяснениями.
Если Вы неплохо знаете английский, то лучше документации, чем та которая распространяется с программой Fractint не найти.
Вопросы можете задавать лично по адресу mailto:sakva@narod.ru
Оставить комментарий
Комментарии














Что это за число n сказать трудно, но можно с большой погрешностью утверждать что это число будет стремиться к величине периметра описанной вокруг (и заведомо большей) острова фигуры, периметр которой мы посчитать можем, например прямоугольника.


А вообше рекомендую знать английский и пользоваться большими ресурсами типа www.sciencedirect.com






Все описанно доступно и понятно для ознакомления с фракталами.


А фишка с екселем совсем потрясная














Формулы скопировал один в один. Напутано однако чего-то.


