Fractal Geometry
Almost all geomtric forms used for building man made objects belong to Euclidean geometry, they are comprised of lines, planes, rectangular volumes, arcs, cylinders, spheres, etc. These elements can be classified as belonging to an integer dimension, either 1, 2, or 3. This concept of dimension can be described both intuitively and mathematically. Intuitively we say that a line is one dimensional because it only takes 1 number to uniquely define any point on it. That one number could be the distance from the start of the line. This applies equally well to the circumference of a circle, a curve, or the boundary of any object.
A plane is two dimensional since in order to uniquely define any point on its surface we require two numbers. There are many ways to arrange the definition of these two numbers but we normally create an orthogonal coordinate system. Other examples of two dimensional objects are the surface of a sphere or an arbitrary twisted plane.
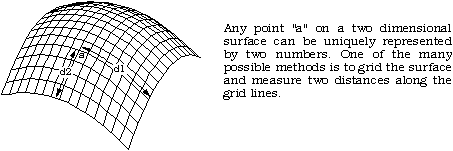
The volume of some solid object is 3 dimensional on the same basis as above, it takes three numbers to uniquely define any point within the object.

A more mathematical description of dimension is based on how the "size" of an object behaves as the linear dimension increases. In one dimension consider a line segment. If the linear dimension of the line segment is doubled then obviously the length (characteristic size) of the line has doubled. In two dimensions, ff the linear dimensions of a rectangle for example is doubled then the characteristic size, the area, increases by a factor of 4. In three dimensions if the linear dimension of a box are doubled then the volume increases by a factor of 8. This relationship between dimension D, linear scaling L and the resulting increase in size S can be generalised and written as
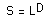
This is just telling us mathematically what we know from everyday experience. If we scale a two dimensional object for example then the area increases by the square of the scaling. If we scale a three dimensional object the volume increases by the cube of the scale factor. Rearranging the above gives an expression for dimension depending on how the size changes as a function of linear scaling, namely
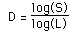
In the examples above the value of D is an integer, either 1, 2, or 3, depending on the dimension of the geometry. This relationship holds for all Euclidean shapes. There are however many shapes which do not conform to the integer based idea of dimension given above in both the intuitive and mathematical descriptions. That is, there are objects which appear to be curves for example but which a point on the curve cannot be uniquely described with just one number. If the earlier scaling formulation for dimension is applied the formula does not yield an integer. There are shapes that lie in a plane but if they are linearly scaled by a factor L, the area does not increase by L squared but by some non integer amount. These geometries are called fractals! One of the simpler fractal shapes is the von Koch snowflake. The method of creating this shape is to repeatedly replace each line segment with the following 4 line segments.

The process starts with a sigle line segment and continues for ever. The first few iterations of this procedure are shown below.
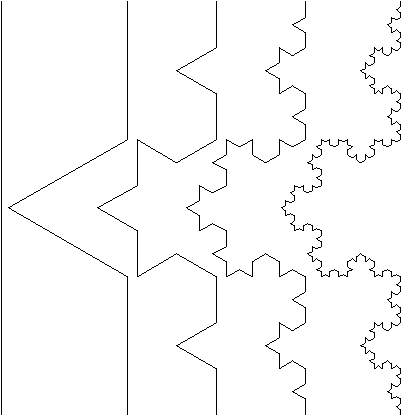
This demonstrates how a very simple generation rule for this shape can generate some unusual (fractal) properties. Unlike Euclidean shapes this object has detail at all levels. If one magnifies an Euclidean shape such as the circumference of a circle it becomes a different shape, namely a striaght line. If we magnify this fractal more and more detail is uncovered, the detail is self similar or rather it is exactly self similar. Put another way, any magnified portion is identical to any other magnified portion.
Note also that the "curve" on the right is not a fractal but only an approximation of one. This is no different from when one draws a circle, it is only an approximation to a perfect circle. At each iteration the length of the curve increases bu a factor of 4/3. Thus the limiting curve is of infinite length and indeed the length between any two points of the curve is infinite. This curve manages to compress an infinite length into a finite area of the plane without intersecting itself! Considering the intuiitve notion of 1 dimensional shapes, although this object appears to be a curve with one starting point and one end point, it is not possible to uniquely specify any position along the curve with one number as we expect to be able to do with Euclidean curves which are 1 dimensional. Although the method of creating this curve is straightforward, there is no algebraic formula the describes the points on the curve. Some of the major differences between fractal and Euclidean geometry are outlined in the following table.

Firstly the recognition of fractal is very modern, they have only formally been studied in the last 10 years compared to Euclidean geometry which goes back over 2000 years. Secondly whereas Euclidean shapes normally have a few characteristic sizes or length scales (eg: the radius of a circle or the length of of a side of a cube) fractals have so characteristic sizes. Fractal shapes are self similar and independent of size or scaling. Third, Euclidean geometry provides a good description of man made objects whereas fractals are required for a representation of naturally occuring geoemtries. It is likely that this limitation of our traditional language of shape is responsible for the stiking difference between mass produced objects and natural shapes. Finally, Euclidean geometries are defined by algebraic formulae, for example
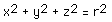
defines a sphere. Fractals are normally the result of a iterative or recursive construction or algorithm.
Оставить комментарий
Комментарии


