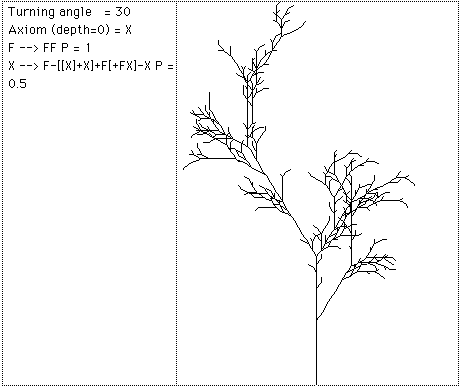
L-Systems
The following is based on L-Systems as described in "Lecture Notes in Biomathematics" by Przemyslaw Prusinkiewcz and James Hanan. A brief description of an 0L system will be presented here but for a more complete description the user should consult the literature.
Simpleminded example of 0L system
A string of characters (symbols) is rewritten on each iteration according to some replacement rules. Consider an initial string (axiom)
and a rewriting rule
After one iteration the following string would result
For the next iteration the same rule is applied but now to the string resulting from the last iteration
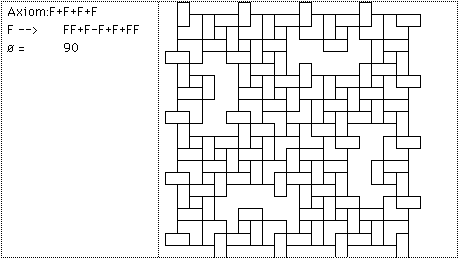
Some symbols are now given a graphical meaning, for example, F means move forward drawing a line, + means turn right by some predefined angle (90 degrees in this case), - means turn left. Using these symbols the initial string F+F+F+F is just a rectangle (? = 90). The replacement rule F --> F+F-F-FF+F+F-F replaces each forward movement by the following figure

The first iteration interpreted graphically is
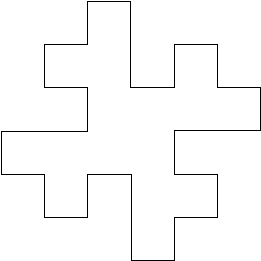
The next iteration interpreted graphically is:
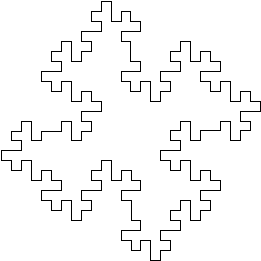
The following characters have a geometric interpretation.

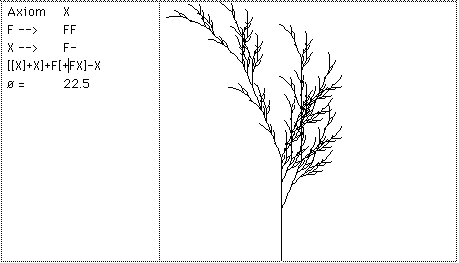
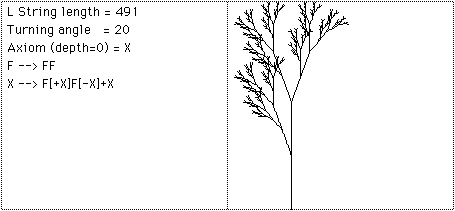
Recent usage of L-Systems is for the creation of realistic looking objects that occur in nature and in particular the branching structure of plants. One of the important characteristics of L systems is that only a small amount of information is required to represent very complex objects. So while the bushes in figure 9 contain many thousands of lines they can be described in a database by only a few bytes of data, the actual bushes are only "grown" when required for visual presentation. Using suitably designed L-System algorithms it is possible to design the L-System production rules that will create a particular class of plant.
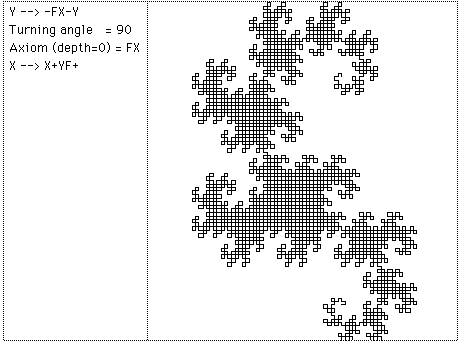
Further examples: