CodeNet / Приложения / Алгоритмы / Графика
CodeNet / Приложения / Графика / 2D

Геометрическое сглаживание В-сплайнами

Любой более или менее сложный чертеж состоит не только из отрезков прямых линий, окружностей и их дуг, но также и из набора кривых линий. Гладкие кривые удобно строить при помощи метода сглаживания кривой типа В-сплайна. B-сплайн это гладкая кривая или, точнее, кривая с непрерывными старшими производными до n-ой, где n порядок сплайна. Заметим, что линия, составленная из В-сплайнов, не будет проходить точно через заданные точки. Подобную кривую составляют из дуг полиномов третьей степени, так как такой полином обеспечивает необходимую непрерывность. Построение линии происходит с помощью итерационной процедуры.

Рассмотрим построение кубического сплайна. Пусть нам даны две соседние точки, через которые проведем кубический полином, но у полинома 4 коэффициента, следовательно нужно еще два дополнительных условия или точки. Для этого прихватим еще две соседние точки. Чем более плавной мы хотим видеть линию, тем сложнее пройти точно через точки. Если в формуле x = q³, то достаточно плавности 3.

Гладкость диктуется физическими задачами, и здесь часто приходится искать компромисс между гладкостью и точностью. Например, гидродинамика работает с поверхностями, которые описываются уравнениями четвертой степени (такой высокий порядок необходим, чтобы повысить гладкость различного рода физических устройств, рассчитанных с помощью этих уравнений, и таким образом избежать завихрений). Но с повышением порядка (то есть гладкости) сплайна точность уменьшается.

Рассмотрим рис. 14.2. Пусть t параметр, по которому пробегаем от точки P_i к точке P_i+1. При t = 0 мы находимся в точке P_i, при t = 1 в точке P_i+1. Если 0 < t < 1, то мы находимся между P_i и P_i+1.

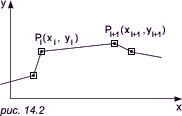
Эта линия в каждой точке имеет систему:

x(t) = ((a₃t + a₂)t + a₁)t + a₀, для 0 <= t <= 1

y(t) = ((b₃t + b₂)t + b₁)t + b₀, для 0 <= t <= 1 a₃ = (-x_i-1 + 3x_i - 3x_i+1 + x_i+2)/6

a₂ = (x_i-1 - 2x_i + x_i+1)/2

a₁ = (-x_i-1 + x_i+1)/2

a₀ = (x_i-1 + 4x_i+ x_i+1)/6

Точки b₃ - b₀ расписывают так же, но вместо x подставляют у. Между P_i и P_i+1 точки а и b не меняются. Если после последней точки указать первую точку, то система замкнет контур.

Достоинства В-сплайна: между точками коэффициенты постоянны; локальное изменение не влечет за собой вычисление заново всего сплайна. Недостатки: могут возникать проблемы при аппроксимации прямой, имеющей разрывы вторых производных (например, сопряжения прямой линии и дуги окружности); с точки зрения эстетики не всегда приемлемы, так как кривизна поверхности, сконструированной с помощью сплайнов, изменяется иногда неравномерно, что приводит к искажениям (например, причудливые искажения предметов, отраженных от кузова автомобиля).

Следствия

Кривые отходят от точек, точки усредняют свое влияние:
x_i: x(0) = a₀ = (x_i-1 + 4x_i + x_i+1)/6
x_i+1: x(1) = a₃ + a₂ + a₁ + a₀ = (x_i + 4x_i+1 + x_i+2)/6
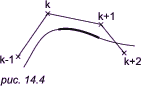
Изменение одной вершины ведет к изменению только четырех соседних отрезков (рис. 14.4).
Геометрическая интерпретация В-сплайна: так как сумма коэффициентов равна единице, а коэффициенты положительны, то мы получаем средневзвешенную точку для четырех соседей, то есть первоначальный отрезок будет находиться внутри выпуклой сплайновой оболочки. Формула расчета: 1/6х_i-1 + 2/3x_i + 1/6x_i+1 = 2/3x_i + 1/3 * [1/2(x_i-1 + x_i+1)]
Кратность вершины усиливает ее притяжение. В острые углы линия не успевает забегать. В этом случае увеличивают кратность вершины. Порядок сплайна влияет на конфигурацию увеличение порядка ведет к большему спрямлению (см. рис. 14.6).

Сглаживание B-сплайнами

Математическое представление тела, составленного из простых геометрических форм (сфер, цилиндров или конусов) несложно. Но очень часто это не так; кузова автомобилей, поверхности самолетов, флюзеляжи и многое другое не так-то просто описать. Процедура, обычно используемая в этих случаях, состоит обычно в следующем:

поверхность покрывается двумя воображаемыми группами линий; первая идет в продольном направлении, вторая трансверсальна к первой. Эта сетка линий определяет множество ячеек, каждая из которых (в случае гладкой поверхности), будет ограничена четырьмя гладкими кривыми;
координаты узлов этой воображаемой сетки измеряются на модели или на наборе чертежей поперечных сечений поверхности;
с помощью интерполяции (усреднения) математически описываются эти две группы линий, образующие сетку.

Можно строить достаточно гладкие кривые и поверхности с использованием полиномов. Допустим, что мы хотим построить поверхность в виде графика функции z = z(x, y). Линия y = const на этой поверхности будет представлена линией z = z(x), она будет проходить через последовательность точек (x₀, z₀), ..., (x_i, z_i), ..., (x_n, z_n) с x₀ < ... < x_i < ... < x_n. Наша цель провести через эти точки составную кривую f(x), имеющую следующие свойства:

на каждом подынтервале x_i-1 <= x <= x_i, i = 1, 2, ..., n функция f(x) является кубическим полиномом;
ее первые и вторые производные непрерывны в узлах.

Полученная гладкая кривая называется кубическим сплайном. Термин «сплайн» возник по аналогии: это название чертежного инструмента тонкой металлической линейки, которая может изгибаться так, чтобы проходить через заданные точки. Физически такая кривая минимизирует энергию внутренних напряжений. Математически имеет минимальную среднеквадратичную кривизну, то есть она наиболее гладкая. Сплайны имеют много приложений в конструировании криволинейных форм. Однако они имеют и некоторые ограничения:

локальное изменение влечет за собой вычисление заново всего сплайна;
могут возникать проблемы при аппроксимации прямой, имеющей разрывы вторых производных (например, сопряжения прямой линии и дуги окружности);
с точки зрения эстетики не всегда приемлемы, так как кривизна поверхности, сконструированной с помощью сплайнов, изменяется иногда неравномерно, что приводит к искажениям (например, причудливые искажения предметов, отраженных от кузова автомобиля).

Первое ограничение можно устранить с помощью B-сплайна. Общая форма полученной в этом случае кривой показана на рис. 20.1.

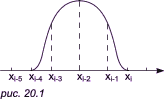
На этом рисунке сплайн продолжен от его конечных точек x_i-4, x_i прямыми линиями, идущими вдоль оси x. В результате получается кубический сплайн на любом числе отрезков, но он не равен нулю только на четырех из них. Такая функция называется B-сплайном (или фундаментальным сплайном) четвертого порядка (или третьей степени). Про него говорят, что он имеет минимальный носитель (носитель это число отрезков, на которых сплайн отличен от нуля).

Заметим, что кубический B-сплайн полностью определяется множеством узлов, на которых он определен, и только одной заданной величиной z. В более общем виде B-сплайн M_mi(x) порядка m (или степени m - 1) на данном множестве узлов везде равен нулю, кроме m последовательных отрезков x_i-m < x < x_i. Опять-таки M_mi(x) определяется множеством узлов и одной величиной z. Принято исключать последнюю степень свободы и фиксировать амплитуду B-сплайна некоторым стандартным образом.

Часто удобно для вычислений использовать нормализованный B-сплайн N_mi(x), связанный с M_mi(x) соотношением N_mi(x) = (x_i - x_i-m)M_mi(x).

Любой сплайн порядка m на множестве узлов x₀, x₁, ..., x_n может быть выражен в виде линейной комбинации B-сплайнов, определенных на том же множестве узлов, расширенном (m - 1) дополнительными узлами на каждом из концов интервала, которые можно выбрать произвольно: x_-m+1, x_-m+2, ..., x_-1 и x_n+1, ..., x_n+m-1. Можно построить m + n - 1 последовательных B-сплайнов на расширенном множестве узлов, каждый из которых отличен от нуля на m последовательных отрезках. Поэтому можно записать:
j(x) = Sc_i * M_mi(x),
где j(x) любой сплайн степени (m - 1) на первоначальном множестве узлов и M_mi(x) есть B-сплайн на расширенном множестве узлов, отличный от нуля при x_i-m < x < x_i; c_i суть числовые коэффициенты; суммирование ведется по i = 1, ..., m + n - 1.

Если имеется множество векторов r₀, r₁, ..., r_n, то можно использовать их: r(u) = Sr_i * N_{4, i+1}(u) (суммирование ведется по i = 0, ..., n). Так как имеется (n + 1) векторных коэффициентов, то необходим набор из (n + 1) B-сплайнов. Последняя формула для 0 <= u <= n - 2 является уравнением кривой, образованной кубическими B-сплайнами.

Свойства

Некоторые простейшие свойства следуют из тождества SN_{4, i+1} = 1, 0 <= u <= n - 2, i = 0..n. При u = 0 следует: r(0) = N₄₂(0)(r₁ - r₀). Из этого следует, что если r₀, r₁, .., r_n вершины некоторой замкнутой ломанной, то кривая, построенная на основе B-сплайна, начинается в r₀ и ее касательная в этой точке имеет направление (r₁ - r₀). Аналогичное утверждение верно и для другого конца. Главное преимущество этого сплайна заключается в том, что изменение одной из вершин влечет за собой изменение только четырех отрезков кривой. Далее, мы также можем построить кривую, аппроксимирующую ломанную с любым желаемым числом сторон. Отрезок сплайна всегда лежит в выпуклой оболочке:

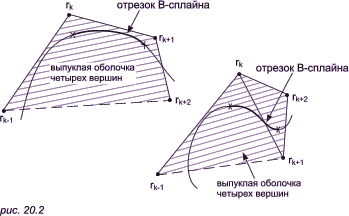
Важным следствием этой выпуклой оболочки является вырождение ее в прямую линию, если 4 последовательные вершины ломанной коллинеарны, значит соответствующий сегмент кривой должен быть прямолинейным.

Имеется еще 2 полезных факта:

кривая проходит вблизи средней точки каждой стороны, за исключением 1-ой и последней точками;
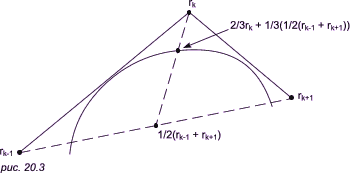
при k = 2, ..., n - 2 кривая проходит через точки: 1/6r_k-1 + 2/3r_k + 1/6r_k+1 = 2/3r_k + 1/3(1/2(r_k-1 + r_k+1))

Эти точки, как показано на рис. 20.3, лежат на 1/3 расстояния от r_k на прямой, соединяющей r_k с серединой отрезка между r_k-1 и r_k+1.

Ваш аккаунт

Последние темы форума

Почтовая рассылка