Метод Рунге-Кутта решения диф. уравнений и их систем.

Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида:

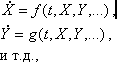
которые имеют решение:

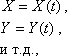
где t - независимая переменная (например, время); X, Y и т.д. - искомые функции (зависимые от t переменные). Функции f, g и т.д. - заданы. Также предполагаются заданными и начальные условия, т.е. значения искомых функций в начальный момент.

Одно диф. уравнение - частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений.

Метод может быть полезен и для решения диф. уравнений высшего (второго и т.д.) порядка, т.к. они могут быть представлены системой диф. уравнений первого порядка.

Метод Рунге-Кутта заключается в рекурентном применении следующих формул:

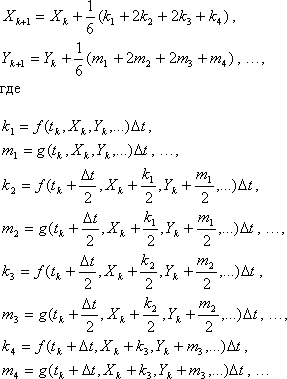
Реализация Метода Рунге-Кутта на Delphi может выглядеть так (привожу полностью модуль):

unit RK_Method;

interface

type
        TVarsArray = array of Extended; // вектор переменных включая независимую
        TInitArray = array of Extended; // вектор начальных значений
        TFunArray = array of function(VarsArray: TVarsArray ):Extended;
        // вектор функций
        TResArray = array of array of Extended; // матрица результатов
        TCoefsArray = array of Extended; // вектор коэффициетов метода

function Runge_Kutt(  // метод Рунге-Кутта
        FunArray: TFunArray; // массив функций
        First: Extended; // начальная точка по независимой координате
        Last: Extended; // конечная точка по независимой координате
        Steps: Integer; // число шагов по независимой координате
        InitArray: TInitArray; // вектор начальных значений
        var Res: TResArray // матрица результатов включая независ. переменную
         ):Word; 
       // возвращаемое значение - код ошибки

implementation

Function Runge_Kutt(  // метод Рунге-Кутта
        FunArray: TFunArray; // массив функций
        First: Extended; // начальная точка по независимой координате
        Last: Extended; // конечная точка по независимой координате
        Steps: Integer; // число шагов по независимой координате
        InitArray: TInitArray; // вектор начальных значений
        var Res: TResArray // матрица результатов включая независ. переменную
         ):Word; // возвращаемое значение - код ошибки
var
        Num: Word; // число уравнений
        NumInit: Word; // число начальных условий
        Delt: Extended; // шаг разбиения
        Vars: TVarsArray; // вектор переменных включая независимую
        Vars2,Vars3,Vars4: TVarsArray; // значения перем. для 2-4 коэф.
        Coefs1: TCoefsArray; // вектор 1-ыx коэффициентов в методе
        Coefs2: TCoefsArray; // вектор 2 коэффициентов в методе
        Coefs3: TCoefsArray; // вектор 3 коэффициентов в методе
        Coefs4: TCoefsArray; // вектор 4 коэффициентов в методе
        I: Integer; // счетчик цикла по иттерациям
        J: Word; // индекс коэф.-тов метода
        K: Integer; // счетчик прочих циклов
begin
 Num:=Length(FunArray); // узнаем число уравнений
 NumInit:=Length(InitArray); // узнаем число начальных условий
 If NumInit<>Num then
   begin
     Result:=100; // код ошибки 100: число уравнений не равно числу нач. усл.
     Exit;
   end;
 Delt:=(Last-First)/Steps; // находим величину шага разбиений
 SetLength(Res,Num+1,Steps+1); // задаем размер матрицы ответов с незав. перем.
 SetLength(Vars,Num+1); // число переменных включая независимую
 SetLength(Vars2,Num+1); // число переменных для 2-го коэф. включая независимую
 SetLength(Vars3,Num+1); // число переменных для 3-го коэф. включая независимую
 SetLength(Vars4,Num+1); // число переменных для 4-го коэф. включая независимую
 SetLength(Coefs1,Num); // число 1-ыx коэф. метода по числу уравнений
 SetLength(Coefs2,Num); // число 2-ыx коэф. метода по числу уравнений
 SetLength(Coefs3,Num); // число 3-иx коэф. метода по числу уравнений
 SetLength(Coefs4,Num); // число 4-ыx коэф. метода по числу уравнений
 // Начальные значения переменных:
 Vars[0]:=First;
 For K:=0 to NumInit-1 do Vars[K+1]:=InitArray[K];
 For J:=0 to Num do Res[J,0]:=Vars[J]; // первая точка результата 
 For I:=0 to Steps-1 do // начало цикла иттераций
        begin
           For J:=0 to Num-1 do Coefs1[J]:=FunArray[J](Vars)*delt; // 1-й коэфф.
           // Находим значения переменных для второго коэф.
           Vars2[0]:=Vars[0]+delt/2;
           For K:=1 to Num do Vars2[K]:=Vars[K]+Coefs1[K-1]/2;
           For J:=0 to Num-1 do Coefs2[J]:=FunArray[J](Vars2)*delt; // 2-й коэф.
           // Находим значения переменных для третьго коэф.
           Vars3[0]:=Vars[0]+delt/2;
           For K:=1 to Num do Vars3[K]:=Vars[K]+Coefs2[K-1]/2;
           For J:=0 to Num-1 do Coefs3[J]:=FunArray[J](Vars3)*delt; // 3 коэфф.
           // Находим значения переменных для 4 коэф.
           Vars4[0]:=Vars[0]+delt;
           For K:=1 to Num do Vars4[K]:=Vars[K]+Coefs3[K-1];
           For J:=0 to Num-1 do Coefs4[J]:=FunArray[J](Vars4)*delt; // 4 коэфф.
           // Находим новые значения переменных включая независимую
           Vars[0]:=Vars[0]+delt;
           For K:=1 to Num do
           Vars[K]:=Vars[K]+
           (1/6)*(Coefs1[K-1]+2*(Coefs2[K-1]+Coefs3[K-1])+Coefs4[K-1]);
           // Результат  иттерации:
           For J:=0 to Num do Res[J,I+1]:=Vars[J];
        end; // конец итераций
 Result:=0; // код ошибки 0 - нет ошибок
end;

end.

Модуль полностью работоспособен. Возвращаемое функцией Runge_Kutt значение - код ошибки. Вы можете дополнить список ошибок по своему усмотрению. Рассчитанные функции системы помещаются в массив Res. Чтобы не загромождать код, в модуле опущены проверки (типа блоков try). Рекомендую их добавить по своему усмотрению.

Ниже приводится описание функции Runge_Kutt и типов, использующихся в модуле.

Function Runge_Kutt (FunArray: TFunArray;
                     First: Extended; 
                     Last: Extended;
                     Steps: Integer;
                     InitArray: TInitArray;
                     var Res: TResArray):Word; 

Здесь:

• FunArray - вектор функций (правых частей уравнений системы);
• First, Last - начальная и конечная точки расчетного интервала;
• Steps - число шагов по расчетному интервалу;
• InitArray - вектор начальных значений
• var Res - матрица результатов включая независимую переменную.

В модуле описаны типы:

type
  TVarsArray = array of Extended; // вектор переменных включая независимую
  TInitArray = array of Extended; // вектор начальных значений
  TFunArray = array of function(VarsArray: TVarsArray ):Extended; // вектор функций
  TResArray = array of array of Extended; // матрица результатов
  TCoefsArray = array of Extended; // вектор коэффициетов метода

Функция возвращает коды ошибок:

• 0 - нет ошибок;
• 100 - число уравнений не равно числу начальных условий.

Решение содержится в переменной-матрице Res. Первый индекс матрицы относится к переменной (0 - независимая переменная, 1 - первая зависимая и т.д.), второй - к номеру расчетной точки (0 - начальная точка).

Рассмотрим один пример использования модуля. Создадим новое приложение и подключим к нему модуль. На форме приложения разместим кнопку Button1 и область текста Memo1. Поместим в приложение две функции и обработчик нажатия кнопки:

//Задаем функции (правые части уравнений)     
function f0(VarArray:TVarsArray):extended;
begin
    Result:=4*VarArray[0]*VarArray[0]*VarArray[0];
end;

function f1(VarArray:TVarsArray):extended;
begin
   Result:=1;
end;

////////////////////////////////////////////////////////////////////////////////

procedure TForm1.Button1Click(Sender: TObject);
var
  I: Integer;
  FunArray: TFunArray; // массив функций
  First: Extended; // начальная точка по независимой координате
  Last: Extended; // конечная точка по независимой координате
  Steps: Integer; // число шагов по независимой координате
  InitArray: TInitArray; // вектор начальных значений
  Res: TResArray; // матрица результатов включая независ. переменную
begin
  // Создаем вектор функций:
  SetLength(FunArray,2);
  FunArray[0]:=f0;
  FunArray[1]:=f1;
  // Задаем интервал и число шагов:
  First:=0;
  Last:=10;
  Steps:=10;
  // Задаем начальные условия:
  SetLength(InitArray,2);
  InitArray[0]:=0;
  InitArray[1]:=0;
  // Вызов метода и получение результатов:
  Memo1.Lines.Clear;
  I:=Runge_Kutt(FunArray, First, Last, Steps, InitArray, Res);
  ShowMessage('Код ошибки = '+IntToStr(I));
  For I:=0 to Steps do
  Memo1.Lines.Add(floattostr(Res[0,I])+'   '+floattostr(Res[1,I])
  +'   '+floattostr(Res[2,I]));
end;

Нажатие кнопки приведет к расчету точек системы, которые будут выведены в текстовую область.

Модуль с примером и справкой можно скачать бесплатно по адресу RK.zip (ZIP, 15,3Kb) (русский вариант). Английский вариант (условно-бесплатный) можно скачать по адресу RK_Eng.zip (ZIP, 23.4Kb)

Ссылки

• http://sadovoya.narod.ru/RK.zip (русский вариант).
• http://sintreseng.narod.ru/RK_Eng.zip (английский, условно-бесплатный вариант)

1.

100.0M

19 октября 2020 года

Аня Чуйкова

0 / / 19.10.2020

19 октября 2020, 11:55:06

Поделитесь пожалуйста учебником, из которого взяты формулы. Спасибо!

2.

97K

15 мая 2016 года

Даша Каленюк

0 / / 15.05.2016

+0 / -1

15 мая 2016, 17:10:03

Скачала по Вашей ссылке русский вариант, изменила для своей системы диф. уравнений, но при запуске выдаёт ошибку :
Project Ex.exe raised exception class EOverflow with message ' Floating point overflow '
Помогите, пожалуйста !!!

Вот изменённый мною модуль:

unit Unit1;
interface
uses
SysUtils, Forms, StdCtrls, Controls, Classes, Dialogs, Math;
type
TForm1 = class(TForm)
Memo1: TMemo;
rk_But: TButton;
procedure rk_ButClick(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
pn,k,ro,Pzv: Extended;

implementation
uses rk_method, Windows;

{$R *.dfm}
procedure Syst (var t: TFloat; var X: TFloatVector;
var RP: TFloatVector);
const
fdr1=0.503;
fdr2=0.503;
fdr3=0.196;
W1=179.8928;
W2=3773.8568;
W3=2504.1203;
b1=55.9203;
b2=98.6;
b3=98.6;
Ls1=3.78;
Ls2=9;
Ls3=15.3;
Svidj2=1352.438;
Svidj3=1352.438;
my=0.62;
vk=30;
m=1.2;
L1=30.969;
L2=42.131;
delta1=0;

begin
pn:=2.5*Power(10,4);
k:=6*Power(10,-7);
ro:=8.5*Power(10,-7);
Pzv:=3.919*Power(10,7);

RP[0] := (1/(k*W1))*(my*fdr1*sqrt(2/ro)*sqrt(Abs(pn-X[0]))-my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-(delta1*delta1*delta1*b1)/(12*ro*vk*Ls1)*X[0]); // dp1/dt
RP[1] := (1/(k*W2))*(my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[4]*X[4]*X[4]*b2)/(12*ro*vk*Ls2)*X[1]); // dp2/dt
RP[2] := (1/(k*W3))*(my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[6]*X[6]*X[6]*b3)/(12*ro*vk*Ls3)*X[2]); // dp3/dt;
RP[3] := (((Svidj2*X[1]*(L1+L2))/L1)-Pzv)*(2/m); // dv2/dt
RP[4] := X[3]; // d delta2/dt
RP[5] := (((Svidj3*X[2]*(L1+L2))/L2)-Pzv)*(2/m); // dv3/dt
RP[6] := X[5]; // d delta3/dt
end;

procedure TForm1.rk_ButClick(Sender: TObject);
var
I, t1, t2: Cardinal;
tOut, InitConds: TFloatVector;
XOuts: TFloatMatrix;
Points: Cardinal;
First, Last: TFloat;
StepsFact: Cardinal;
Count: Word;
begin
Memo1.Clear;
First := 0.0;
Last := 10.0;
Count:= 7;
Points:=10+1; //11 points for output
StepsFact:=1000000; //all steps inside function = 10*StepsFact

try
SetLength(InitConds, Count);
InitConds[0]:=0.0; //x0(0)=0
InitConds[1]:=0.0; //x1(0)=0
InitConds[2]:=0.0; //x2(0)=0
InitConds[3]:=0.0; //x3(0)=0
InitConds[4]:=0.0; //x4(0)=0
InitConds[5]:=0.0; //x5(0)=0
InitConds[6]:=0.0; //x6(0)=0

SetLength(tOut, Points);
SetLength(XOuts, Count, Points);
except
ShowMessage('Out of memory!!!');
exit;
end;

t1:= GetTickCount();
I := rk4fixed( Syst, InitConds, First, Last, tOut, XOuts, StepsFact );
t2:= GetTickCount();
Memo1.Lines.Add('Error Code = ' + IntToStr(I));
Memo1.Lines.Add('Run time, ms = ' + IntToStr(t2-t1));
Memo1.Lines.Add('');
if I = 0 then
for I := 0 to Points - 1 do
Memo1.Lines.Add(
't = '+ FloatToStr(TOut)+
' x0 = '+ FloatToStr(XOuts[0, I])+
' x1 = '+ FloatToStr(XOuts[1, I])+
' x2 = '+ FloatToStr(XOuts[2, I])+
' x3 = '+ FloatToStr(XOuts[3, I])+
' x4 = '+ FloatToStr(XOuts[4, I])+
' x5 = '+ FloatToStr(XOuts[5, I])+
' x6 = '+ FloatToStr(XOuts[6, I])
);
//Clean memory:
XOuts := Nil; tOut := Nil; InitConds := Nil;
end;
end.

3.

326

19 ноября 2005 года

sadovoya

757 / / 19.11.2005

24 февраля 2015, 20:40:10

Обновления модуля для Delphi и Lazarus можно найти на странице http://sadovoya.narod.ru/codes.htm либо в исходниках в этом форуме. Там-же есть обновленный вариант для C++.

Автор

4.

91K

11 июня 2013 года

Александр Янак

0 / / 11.06.2013

+1 / -0

11 июня 2013, 03:24:45

ребята, а на Pascal кто нить может реализовать?

5.

326

19 ноября 2005 года

sadovoya

757 / / 19.11.2005

+3 / -1

4 августа 2011, 17:18:37

Кому интересно -- вот реализация Рунге-Кутта на C++. Одним файлом: сам метод и пример для консоли.

#include <iostream>

using namespace std;

#define DEFAULT_STEPS 1000

unsigned short rk(double (*rightParts[])(double,double[]),
const double initConds[], unsigned int count, double first, double last,
double unDependVarPoints[], double *dependVarsRes[],
unsigned int steps = DEFAULT_STEPS)
{

if (last < first) return 2000;
if (!steps) return 3000;
if (!count) return 4000;

unsigned int i, j, points = steps + 1;

try{
for(j = 0; j < count; ++j)
dependVarsRes[j] = new double [points]; //get memory
}
catch(...){return 1000;}

try{

double tVar, delt = (last - first)/steps;
double xVars[4][count];
double c[4][count];

// Initial values of vars and first point of results:
for(j = 0; j < count; ++j){
xVars[0][j] = initConds[j];
dependVarsRes[j][0] = xVars[0][j];
}
tVar = first;
unDependVarPoints[0] = tVar;

for(i = 0; i < steps; ++i){
// itterations begin
for (j = 0; j < count; ++j){
c[0][j] = rightParts[j](tVar, xVars[0])*delt;
// Get values of vars for c[1]:
xVars[1][j] = xVars[0][j] + c[0][j]/2.0;
}
tVar += delt/2.0;
for (j = 0; j < count; ++j){
c[1][j] = rightParts[j](tVar, xVars[1])*delt;
// Get values of vars for c[2]:
xVars[2][j] = xVars[0][j] + c[1][j]/2.0;
}
for (j = 0; j < count; ++j){
c[2][j] = rightParts[j](tVar, xVars[2])*delt;
// Get values of vars for c[3]:
xVars[3][j] = xVars[0][j] + c[2][j];
}
tVar += delt/2.0;
for (j = 0; j < count; ++j){
c[3][j] = rightParts[j](tVar, xVars[3])*delt;
// Get new values of vars (and Itteration result):
dependVarsRes[j][i+1] = xVars[0][j] +=
(c[0][j] + 2.0*(c[1][j] + c[2][j]) + c[3][j])/6.0;
}
unDependVarPoints[i+1] = tVar;
} // Itterations end

}//try

catch(...){return 5000;} //а очищать память будет вызывающая программа

return 0;//ok
}



double f0(double t, double x[]){
return 2*t;
}

double f1(double t, double x[]){
return 3*x[0];
}

int main()
{
unsigned int num = 2, st, points, dst;
double (*fun[])(double,double[]) = {f0,f1};
double iC[] = {0.0,0.0};
double t0 = 0.0, te = 10.0;
double *dVP[num];

rep:

cout << "Enter number of steps (min 10)\n";
cin >> st;
if (st < 10) goto rep;
dst = st/10;

points = st + 1;
double *uDVP;
try{uDVP = new double [points];}
catch(...) {cout << "Error: array is too big...\n" << endl; return -1;}

unsigned short erc = rk(fun,iC,num,t0,te,uDVP,dVP,st);
if (!erc){
cout << "Returned with no errors\n\n ";
for(unsigned int i = 0; i < points; i += dst){
cout << uDVP << '\t' << dVP[0] << '\t' << dVP[1] << endl;
}
}
else cout << "Returned code is " << erc << endl;

delete [] uDVP;
for(unsigned int i = 0; i < num; ++i) delete[] dVP; //free memory

char ch;
cout << "\nRepiat? [1/0]\n";
cin >> ch;

if (ch == '1') goto rep;

return 0;
}

6.

326

19 ноября 2005 года

sadovoya

757 / / 19.11.2005

+2 / -0

19 марта 2011, 15:59:29

Надо бы еще выделенную под динамические массивы память освобождать в функции модуля и в вызывающей программе. Исправленные исходники выложены на этом сайте, как для Дельфи, так и для Лазарус. Также можно скачать и с моего сайта.

Автор.

7.

60K

25 апреля 2010 года

artecovez

0 / / 25.04.2010

+1 / -0

25 апреля 2010, 13:32:29

а кто-нит ьможет подсказать,как задать систему для решения диффура второг опорядка на языке С++???очень надо..

8.

60K

06 апреля 2010 года

huns

0 / / 06.04.2010

6 апреля 2010, 00:16:47

По поводу высших порядков)) все очень просто: все тоже самое, только получаем "n" уравнений, где "n" - это порядок. т.е. x1=x2`,x2=x3`, x3=x4` ... и т.д.

9.

46K

25 декабря 2008 года

Zhuma

0 / / 25.12.2008

+3 / -0

25 декабря 2008, 23:28:20

Zhuma / Благодарю автора и создателей проекта CodeNet за ваш труд, ну и пусть вознаградятся ваши усилия!!!

10.

44K

28 октября 2008 года

Саша-3000

0 / / 28.10.2008

+0 / -1

28 октября 2008, 18:55:13

Вот такой вопрос. Почему нет реализаций более высоких порядков?

11.

37K

05 марта 2008 года

Bisengaliev Renat

0 / / 05.03.2008

+1 / -0

5 марта 2008, 17:12:56

Здравствуйте.
А нет ли текста программы для алгоритма Рунге - Кутта на языке Fortran?

12.

19K

28 июня 2006 года

sugar

0 / / 28.06.2006

28 июня 2006, 17:23:25

А что надо изменить, если нужен рунге-кутта 2 порядка?

13.

Аноним

+3 / -1

5 мая 2006, 23:46:25

Пасиб большое!!! Благодаря вам я лабораторку СДАЛ!!! И вообще отличный сайт. Нашел кучу всего нужного и полезного.

14.

Аноним

+2 / -1

5 мая 2006, 23:37:32

Пасиб большое!!! Благодаря вам я лабораторку СДАЛ!!!

15.

Аноним

+2 / -1

22 марта 2006, 23:44:30

Да, скольких студентов эта статья от головной боли избавит! И что ж она раньше не появилась, когда я подобную задачу решал, ведь кстати говоря, многие источники приводят и описывают ментод Р-К только 1-го порядка.