What is a fractal?

B. Mandelbrot:A rough or fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole.

Mathematical:A set of points whose fractal dimension exceeds its topological dimension.

Chaotic Systems

The classic Mandelbrot below has been the image that has greatly popularised chaotic and fractal systems. The Mandelbrot set is created by a general technique where a function of the form z_n+1 = f(z_n) is used to create a series of a complex variable. In the case of the Mandelbrot the function is f(z_n) = z_n² + z_o. This series in generated for every initial point z_o on some partition of the complex plane. To draw an image on a computer screen the point under consideration is coloured depending on the behaviour of the series which will act in one of the following ways:

1. decay to 0
2. tend to infinity
3. oscillate among a number of states
4. exhibits no discernible pattern

In the figure above, situation (a) occurs in the interior portion, (b) in the exterior, (c) and (d) near the boundary. The boundary of the set exhibits infinite detail and variation (the boundary will never appear smooth irrespective of the zoom factor), as well as self similarity.

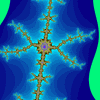
An example using the same technique but a different function is called "biomorphs" by C.A.Pickover. It uses the function f(z_n) = sin(z_n) + z_n² + c and gives rise to many biological looking creatures depending on the value of the constant "c".