Strange Attractors

A second technique, often called "hopalong", is normally used to represent the strange attractor of a chaotic system, for example, the well known Julia set. In this case each coordinate generated by the series is drawn as a small point, ie: we hop-along from one point to the next. For an image on a plane the series is either an equation of a complex variable or else there are two interrelated equations, one for the x and one for the y coordinate. As an example consider the following function:

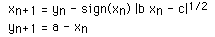
This series of x,y coordinates is specified by an initial point x_o,y_o and three constants a,b, and c. The following is an example where a=0.4, b=1, and c=0.

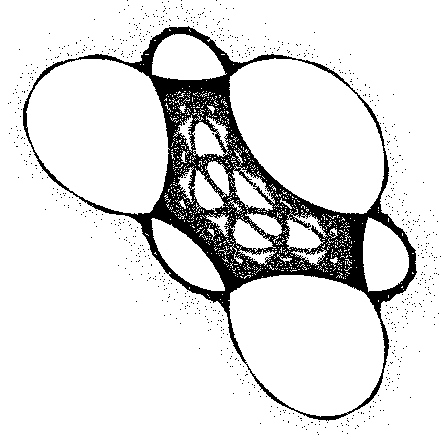
Interestingly for strange attractors the initial point does not matter (except for a few special cases), ie: all initial coordinates x_o,y_o result in the same image. In other words, the image shows the x,y pairs that can be generated by the series, any initial point will generate the same set of points although they will be generated in a different order. Another example attributed to Peter de Jong uses the two equations

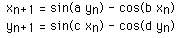
This gives swirling tendrils that appear three dimensional, an example is shown below where a = -2.24, b = -0.65, c = 0.43, d = -2.43.

1.

Аноним

27 июня 2005, 21:57:09

Hi im just a beginner in this .. in fact i started to studymathematics 1 year ago ... so maybe my question can be trivial for you
is ther more information about how this functions are generated and the properties of recursion and invertibility... ??
for example butterfly of lorenz and strange attractors...
are they always invertible if they are differntiable in all points ??? ... if i start in a point x0 .. then i iterate the function then the x0 moves the trajectory to x0'... is there any way to return to x0 ? with a function using the same codomain and domains ?

Thanks and sorry for my english :p

Eduardo Ruiz Duarte