Newton Raphson

This technique is based on the Newton Raphson method of finding the solution (roots) to a polynomial equation of the form

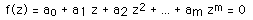
The method generates a series where the n+1'th approximation to the solution is given by

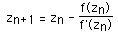
where f'(z_n) is the slope (first derivative) of f(z) evaluated at z_n. To create a 2D image using this technique each point in a partition of the plane is used as initial guess, z_o, to the solution. The point is coloured depending on which solution is found and/or how long it took to arrive at the solution. A simple example is an application of the above to find the three roots of the polynomial z*z*z - 1 = 0. The following shows the appearance of a small portion of the positive real and imaginary quadrant of the complex plane. A trademark of chaotic systems is that very similar initial conditions can give rise to very different behaviour. In the image shown there are points very close together one of which converges to the solution very fast and the other converges very slowly.