CodeNet / Приложения / Алгоритмы / Сжатие и кодирование
CodeNet / Приложения / Графика / Форматы файлов
CodeNet / Остальное / Форматы файлов
Формат JPEG
Алгоритм JPEG
В алгоритме JPEG исходное изображение представляется двумерной матрицей размера N*N, элементами которой являются цвет или яркость пиксела. Упаковка значений матрицы выполняется за три этапа.
Высокая эффективность сжатия, которую дает этот алгоритм, основана на том факте, что в матрице частотных коэффициентов, образующейся из исходной матрицы после дискретного косинусного преобразования, низкочастотные компоненты расположены ближе к левому верхнему углу, а высокочастотные - внизу справа. Это важно потому, что большинство графических образов на экране компьютера состоит из низкочастотной информации, так что высокочастотные компоненты матрицы можно безболезненно выбросить.“Выбрасывание” выполняется путем округления частотных коэффициентов. После округления отличные от нуля значения низкочастотных компонент остаются, главным образом, в левом верхнем углу матрицы. Округленная матрица значений кодируется с учетом повторов нулей. В результате графический образ сжимается более чем на 90% , теряя очень немного в качестве изображения только на этапе округления.
Дискретное косинус преобразование
Основным этапом работы алгоритма является дискретное косинусное преобразование (ДКП), представляющее собой разновидность преобразования Фурье. Оно позволяет переходить от пространственного представления изображения к его спектральному представлению и обратно. Что нужно сделать на первом этапе первом этапе ? Следует создать ДКП матрицу, используя такую формулу :
DCT = 1/sqr(N), если i=0
ij
DCT = sqr(2/N)*cos[(2j+1)*i*3.14/2N], если i > 0
ij
N = 8, 0
в результате имеем:
|.353553 .353553 .353553 .353553 .353553 .353553 .353553 .353553|
|.490393 .415818 .277992 .097887 -.097106 -.277329 -.415375 -.490246|
|.461978 .191618 -.190882 -.461673 -.462282 -.192353 .190145 .461366|
DCT = |.414818 -.097106 -.490246 -.278653 .276667 .490710 .099448 -.414486|
|.353694 -.353131 -.354256 .352567 .354819 -.352001 -.355378 .351435|
|.277992 -.490246 .096324 .416700 -.414486 -.100228 .491013 -.274673|
|.191618 -.462282 .461366 -.189409 -.193822 .463187 -.460440 .187195|
|.097887 -.278653 .416700 -.490862 .489771 -.413593 .274008 -.092414|
например, нам нужно сжать следующий фрагмент изображения:
| 95 88 88 87 95 88 95 95|
|143 144 151 151 153 170 183 181|
|153 151 162 166 162 151 126 117|
IMG = |143 144 133 130 143 153 159 175|
|123 112 116 130 143 147 162 189|
|133 151 162 166 170 188 166 128|
|160 168 166 159 135 101 93 98|
|154 155 153 144 126 106 118 133|
|-33 -40 -40 -41 -33 -40 -33 -33|
| 15 16 23 23 25 42 55 53|
| 25 23 34 38 34 23 -2 -11|
IMG = | 15 16 5 2 15 25 31 47|
| -5 -16 -12 2 15 19 34 61|
| 5 23 34 38 42 60 38 0|
| 32 40 38 31 7 -27 -35 -30|
| 26 27 25 16 -2 -22 -10 5|
T
вот формула, по которой производится ДКП: RES*IMG*DCT
T
для начала нужно посчитать промежуточную матрицу: TMP = IMG*DCT
|-103 -3 1 2 4 0 -1 5|
| 89 -40 12 -2 -7 5 1 0|
| 57 31 -30 6 2 0 5 0|
TMP = | 55 -28 24 1 0 -8 0 0|
| 32 -60 18 -1 14 0 -8 1|
| 84 -11 -37 17 -24 4 0 -4|
| 19 81 -16 -20 8 -3 4 0|
| 22 40 11 -22 8 0 -3 2|
затем умножаем ее на ДКП матрицу: RES = TMP*DCT
| 91 3 -5 -6 2 0 1|
|-38 -57 9 17 -2 2 2|
|-80 58 0 -18 4 3 4|
RES = |-52 -36 -11 13 -9 3 0|
|-86 -40 44 -7 17 -6 4|
|-62 64 -13 -1 3 -8 0|
|-16 14 -35 17 -11 2 -1|
|-53 32 -9 -8 22 0 2|
Этап Квантования
На этом этапе мы посчитаем матрицу квантования, используя этот псевдо код:
for i:=0 to 8 do
for j:=0 to 8 do
Q[i,j] = 1+((1+i+j)*q);
где q - это коэффициент качества, от него зависит степень потери качества сжатого изображения для q = 2 имеем матрицу квантования:
| 3 5 7 9 11 13 15 17|
| 5 7 9 11 13 15 17 19|
| 7 9 11 13 15 17 19 21|
Q = | 9 11 13 15 17 19 21 23|
|11 13 15 17 19 21 23 25|
|13 15 17 19 21 23 25 27|
|15 17 19 21 23 25 27 29|
|17 19 21 23 25 27 29 31|
теперь нужно каждое число в матрице квантования разделить на число в соответствущей позиции в матрице RES, в результате получим:
| 30 0 0 0 0 0 0 0|
| -7 8 1 1 0 0 0 0|
|-11 6 0 1 0 0 0 0|
A = | -5 -3 0 0 0 0 0 0|
| -7 -3 2 0 0 0 0 0|
| -4 4 0 0 0 0 0 0|
| -1 0 1 0 0 0 0 0|
| -3 1 0 0 0 0 0 0|
как вы видите здесь имеется довольно много нулей, мы получим наиболее длинную последовательность нулей, если будем использовать следущий алгоритм:
+----+----+----+----+----+----+----+----+
| 1 | 2 | 6 | 7 | 15 | 16 | 28 | 29 |
+----+----+----+----+----+----+----+----+
| 3 | 5 | 8 | 14 | 17 | 27 | 30 | 43 |
+----+----+----+----+----+----+----+----+
| 4 | 9 | 13 | 18 | 26 | 31 | 42 | 44 |
+----+----+----+----+----+----+----+----+
| 10 | 12 | 19 | 25 | 32 | 41 | 45 | 54 |
+----+----+----+----+----+----+----+----+
| 11 | 20 | 24 | 33 | 40 | 46 | 53 | 55 |
+----+----+----+----+----+----+----+----+
| 21 | 23 | 34 | 39 | 47 | 52 | 56 | 61 |
+----+----+----+----+----+----+----+----+
| 22 | 35 | 38 | 48 | 51 | 57 | 60 | 62 |
+----+----+----+----+----+----+----+----+
| 36 | 37 | 49 | 50 | 58 | 59 | 63 | 64 |
+----+----+----+----+----+----+----+----+
итак у нас получилась последовательность:
30 0 -7 -11 8 0 0 1 6 -5 -7 -3 0 1 0 0 0 1 0 -3 -4 -1 4 2 0 0 0 0
0 0 0 0 0 0 0 -3 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Этап Вторичного Сжатия.
Самым распространенным методом вторичного сжатия является метод Хаффмана и его разновидности.
Метод Хаффмана.
Сжатие Хаффмана - статистический метод сжатия, который уменьшает среднюю длину кодового слова для символов алфавита. Код Хаффмана является примером кода, оптимального в случае, когда все вероятности появления символов в сообщении - целые отри- цательные степени двойки. Код Хаффмана может быть построен по следующему алгоритму:
- Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте;
- Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагается равной сумме вероятностей составляющих его символов. В конце концов, мы построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него;
- Прослеживаем путь к каждому листу дерева помечая направление к каждому узлу (например, направо - 1, налево - 0).
Поясним создание дерева с использованием иллюстраций :
A B C D E
10 5 8 13 10
B C A E D
5 8 10 10 13
A E BC D
10 10 13 13
BC D AE
13 13 20
AE BCD
20 26
AEBCD
46
Таким образом, построено дерево
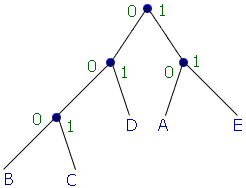
Теперь, если в тексте встречается, например, символ "d", то вместо того, чтобы выделять этому символу байт, после сжатия символ займет всего 2 бита (01).
Оставить комментарий
Комментарии




Y = (1/4)*DCT*X*DCTT - преобразованая
X = (1/4)*DCTT*X*DCT - обратное преобразование
DCT(i,j) = dct(i,j)
DCTT(i,j) = dct(j,i)
double dct(int i, int j){
if (i == 0)
f = 1/sqrt(2.);
return f1*cos(i*(((1 + 2*j)*Pi)/(2*N)));
}
Проверено, работает.






дополню только тем, что тут описано ядро для ч/б картинок...
для цветных.. перед ДКП осуществляется еще пара штуковин.. перечислю скрупулезно... мало ли:)
1. Переход от RGB к YCrCb
2. Субдискретизация по стандарту 4:1:1 (на 4 отсчета уровня яркости Y берется по одному отсчету цветоразностных Cr и Cb)
3. Разбиение полученной каши на фрагменты 8х8
далее идет ДКП... квантование... zig-zag-образное сканирование полученных фрагментов.... кодирование по Хафману.




не
"... нужно каждое число в матрице квантования разделить на число в соответствущей позиции в матрице RES..."
а наоборот - Res на Q .



